Update, 20 October 2023: I no longer stand by the ideas in this post. The fundamental problem with time allocation is that capital is higher leverage than time, and so investing ideas often don’t map to career decision making.
Last week we looked at the Kelly Criterion as a method for evaluating bets you make with your time — partly because it’s the optimal method for optimising capital growth, but partly because I found it so bloody cool that I couldn’t help myself.
The problem with the Kelly Criterion, however, is that I haven’t figured out how to make it work when applied to time management. The Kelly formula depends on a number of assumptions, not of all which hold true when applied to our lives.
(If you’re new to this idea of approaching time management as a bet allocation exercise, here’s the short summary: when you decide to spend time on a task, you’re essentially making a bet under uncertainty. You’re not sure if your chosen activity would give you the career/life outcomes you desire. How do you allocate your time to a portfolio of different activities? This series of posts is basically me figuring out if we could take ideas from finance and decision-making and adapt it for daily time management. You should probably read the first post for a basic explanation).
This week, we’ll look at something more immediately practical: the idea of using a stochastic decision process to evaluate bets with time.
The Setup
Imagine that you have a project you’re working on that consists of three sub-tasks. Task B depends on Task A being completed. In order to finish the project successfully, you would need to execute all three tasks A, B and C successfully; the failure of any one task means your entire project fails.
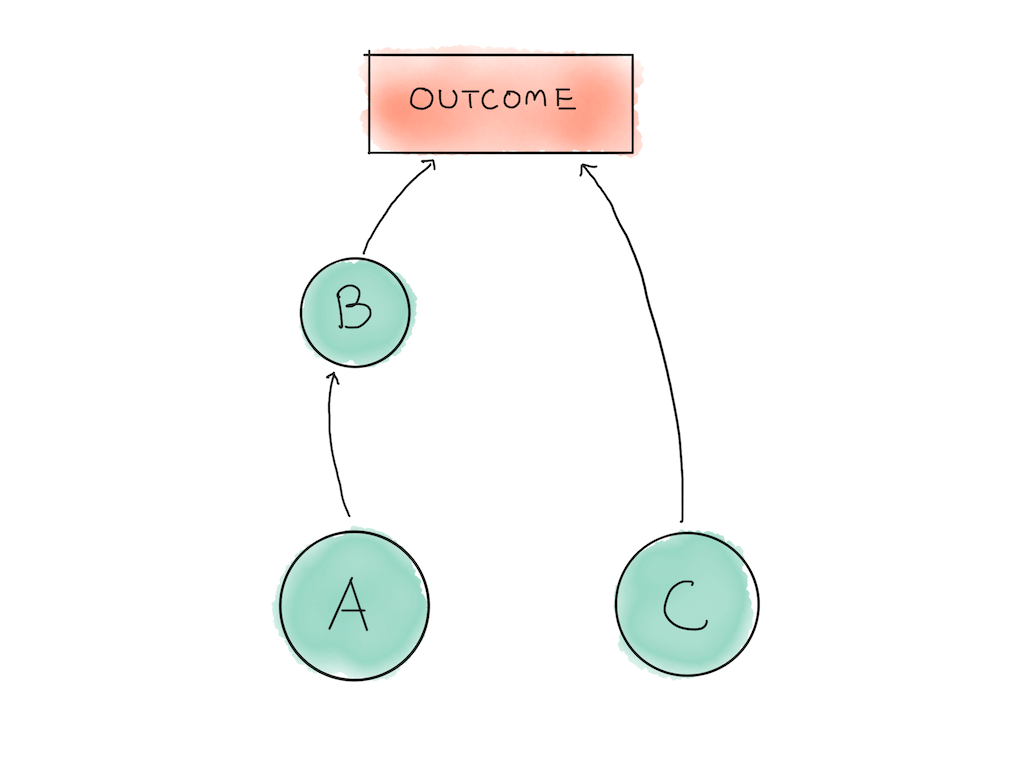
This is similar to many real world projects.
Say that you’re running an online shoe store. You could run ads to direct new visitors to your website, which requires you to write the copy and prepare a landing page and set up the ad campaign in Google. One project, many sub-tasks.
Or you could go after running clubs and sponsor their meetups. This requires you to research meetup events and pack your wares and prepare your pitch.
Each initiative consists of multiple smaller steps, some of which might fail. Which project is a better bet? This question works at the level of entire projects, but also at the level of individual tasks that make up that project: certain steps give you information about the feasibility of tackling the project in the first place.
So what do we do?
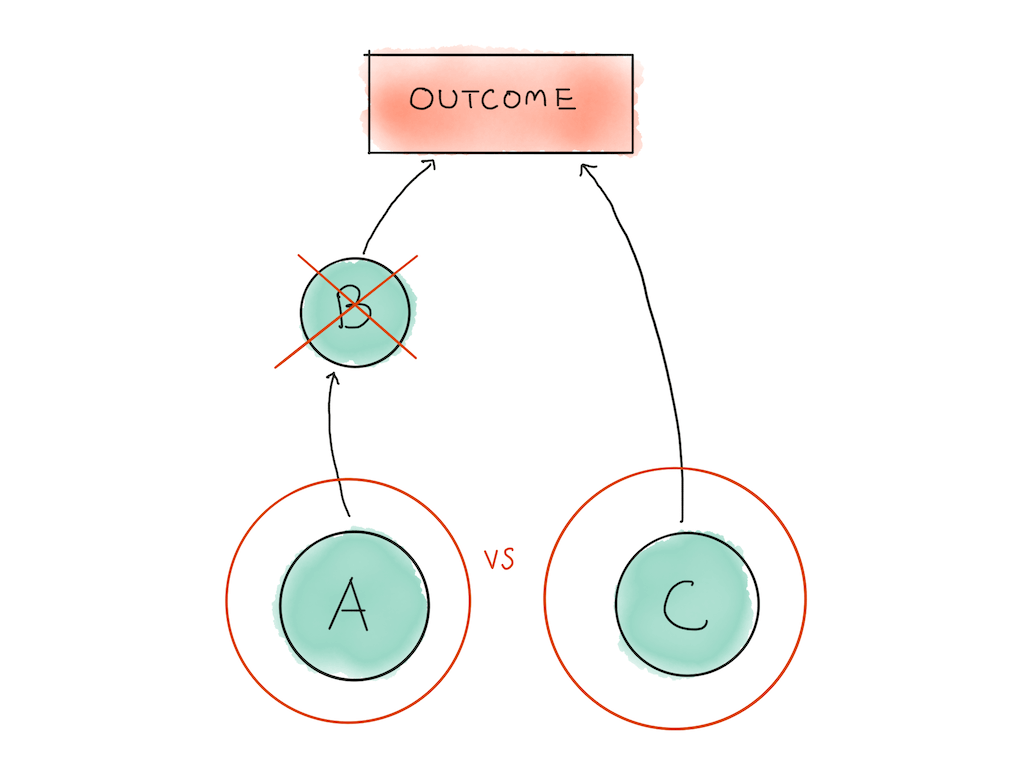
We’ll start with the obvious things: task B depends on task A’s completion, which means that we can ignore it for now. The time allocation decision you have to make is between task A and task C.
One obvious way many of us think about tasks is by reasoning about how long each task would take, and how difficult that task is to do. So let’s pretend that task A is something you know how to do — it takes 30 minutes and you judge that it has a 90% probability of success. Task C, on the other hand, is something you’ve never done before — it takes 4 hours and has a 40% probability of success.
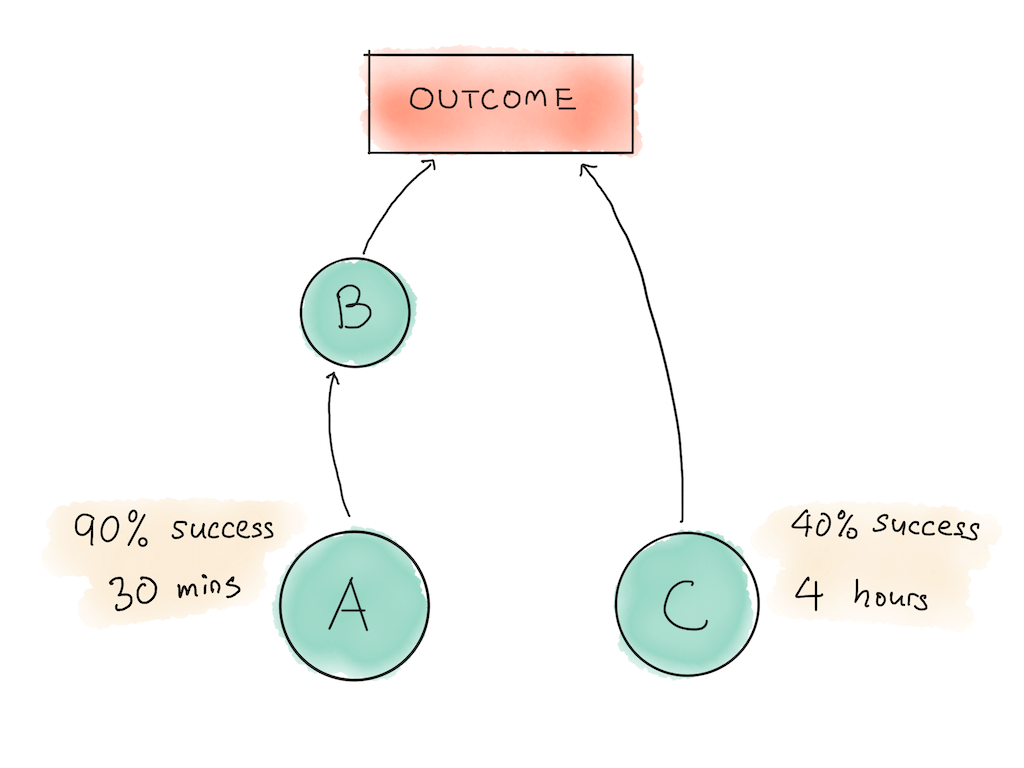
Which of these tasks do you work on first?
What Not To Do
The naive approach here is to do what feels right. This is occasionally a valid strategy! In many domains, the environment is regular enough that practitioners build an intuitive ability to prioritise tasks; this ability comes naturally from expertise (see more on this effect here). In my domain of software engineering, good product managers eventually get good at evaluating the order of tasks to tackle in a large software project. The key word here is eventually — and only on tasks in domains they have experience with.
This strategy has two flaws: first, when you’re just starting out, you don’t have a good feel for task prioritisation. Some tasks are more important than others, in the sense that they are more critical to the execution of your plan. You nearly always want to do the critical tasks first.
Second, when you’re dealing with tasks outside your circle of competence, the intuition-first approach will fail. This is also true within specific fields, like my field of software engineering! In my case, I have a pretty good sense for most web-app-related software engineering tasks, but I’m simply terrible when it comes to managing large-scale server infrastructure projects (and, honestly speaking, anything else outside that circle of competence). It wouldn’t be prudent for me to rely on my intuition on subdomains I have little experience with.
Alright, so what else could we do? One intuitive approach many of people take is to tackle the components in an increasing order of difficulty. That is: do the easiest tasks first, build momentum, and eventually tackle the hardest tasks near the end of the project. This is psychologically very attractive, with at least one major benefit: it staves off procrastination by making the entire project easier to approach.
What’s wrong with this strategy? Well, sooner or later, you’ll hit a difficult component and discover that your current approach doesn’t work. This forces you to throw away all the ‘easy’ work you’ve completed up to that point. In some cases, this easy work is reusable; in others, you have to restart from scratch because your progress depends on an assumption captured in the difficult task.
Do The Risky Thing First
At this point experienced project managers are probably shouting: “do the risky thing first!” This is directionally correct. The motivation here is that if you do the risky bits earlier in the project timeline, you’ll be more likely to course-correct and pick a successful execution path when things go wrong. Better still, you won’t waste time on approaches or projects that just can’t work!
‘Do the risky thing first’ translates to ‘pick tasks that are more likely to fail and do them first’. Doing such riskier tasks gives you information about your current approach. If a particular task fails, you could save time by picking another direction (or discarding the project for a more promising one). But information alone isn’t all that matters — you should also take into account the time needed to gain that information.
In a nutshell, your strategy now becomes: do the tasks in order from the most informative per unit time to the least informative per unit time.
In order to do this, you’ll need a way to quantify informativeness. Jacob Steinhardt, from whom this technique is taken, proposes two methods to do just that.
Informativeness Definition 1: Expected Time Saved
If an early task fails, you could save time by not having to attempt later steps. Let’s take our earlier scenario as an example:

In our scenario above, it makes more sense to attempt Task A instead of Task C, because if Task A fails you save 240 minutes (which means 0.1 x 240 = 24 minutes in expectation). Whereas if you did task C first and it failed, you would have only saved 30 minutes (0.6 x 30 = 18 minutes in expectation). Because 24 minutes in expectation > 18 minutes in expectation, you would expect to get more information from attempting Task A over Task C.
Two important caveats: this method assumes that you need to complete the task before you know if it succeeds; in practice you’re likely to encounter a blocker during the expected time required to finish the task.
What I’ve done in such cases is to estimate the time taken to discover blockers — that is, how long I would expect it to take before I learn about the feasibility of the task. For programming work, this might sometimes be in the very first hour of reading about a problem; in other cases it takes half a day of prototyping before I realise that my approach is fundamentally broken.
The second caveat is that this method only allows you to compare between two tasks. Anything more and you’ll be required to make n! permutations, as you would have to compare every task with every other task. This problem is solved with the next approach.
Informativeness Definition 2: Failure Rate
Imagine that you’re working on Task C (4 hours, 40% probability of success). One way of reasoning about failure is that the 60% chance of failing might occur during any one of those 240 minutes. Or, to phrase this differently, for each minute you spend on task C, an approximately 0.25% chance exists that the failure would occur in that particular minute.
This treats the occurrence of failure as a Poisson arrival process, which then means that we can model the time at which a failure occurs using an exponential distribution with a rate parameter \(\lambda\). Using basic properties of a Poisson process, \(\lambda\) may be computed as:
$$\lambda = \frac{log(\frac{1}{p})}{T}$$Where \(p\) is the success probability of the task and \(T\) is the time taken. This rate, \(\lambda\), tells us how quickly you should expect to encounter failures while doing a given task. Because you want to prioritise tasks with an earlier probability of failure, you should rank your tasks in the order of \(\lambda\).
So let’s work out our example above:
$$ Task A: \lambda = \frac{log(\frac{1}{0.9})}{0.5} = 0.21 \\ Task C: \lambda = \frac{log(\frac{1}{0.4})}{4} = 0.23 $$Task C has a higher rate, so it’s actually slightly better to do it first! The alert reader might also notice that this result is the opposite of the previous method, and the reason is because the higher the probability of failure, the earlier we should expect to encounter that failure in a Poisson process.
This rate method is better than the first method because it can be used for more than two tasks: you merely have to calculate \(\lambda\) for all the tasks and rank them from highest to lowest. The only problem is that it assumes you’ll encounter the failure during execution of a task (while the first method assumes you’ll only find out at the end of the allocated task time) — in practice, failure might occur both ways.
Summary and Some Caveats
As I’ve mentioned earlier, this idea is lifted nearly verbatim from Jacob Steinhardt’s essay Research as a Stochastic Decision Process. At the time of writing it Steinhardt was a graduate student at Stanford, and developed these methods to increase his research productivity. I was so taken by his ideas that I immediately put them to practice with my projects; I present the two methods here in an easier-to-read format for fear that his Stanford website would be deleted.
I recommend reading the entire essay if you are interested in research or if you want to peek at the math behind these formulas.
Why do these methods work?
I think a key point to remember is that Steinhardt's two methods have to do with bets of high uncertainty. The human brain doesn’t deal well with high levels of uncertainty. If I walked up to you and asked you to bet some of your money on a wager, you would stop for a bit and immediately shift to an analytical frame of mind. At which point your System 1 brain goes “STOP, DON’T WASTE ENERGY” and substitutes proper analysis for intuition.
We are not evolved to handle probability judgments, so we drop down to heuristics and gut-feel.
In regular environments, such intuitions are useful. And in fact my earlier observation about product managers in the software world hold true: you can certainly build an intuitive sense of risk in software development, which leads to effective prioritisation. But in high uncertainty areas — such as, say, an entrepreneur picking an idea to test, or a scientist picking a research direction, good intuitions are much harder to come by. It pays to use these methods as guard rails for thought.
I think it’s clear that these two methods depend on having good probability judgments. A friend of mine in research immediately objected to the false precision of using probability values. “How do you know that your probability isn’t pulled from thin air?” he asked.
This misses the point, I think. We make probability judgments all the time — in fact, think back to the last time you made a decision that required you to pick between two activities. I’m willing to bet that you used a fuzzy sense of outcome likelihood to decide; you then rationalised to yourself that your chosen path ‘is the better one to take’, or something similar.
My take is that if you’re going to make such judgments anyway, you should probably make them in the context of a thoughtful framework. And that, I think, gets at the heart of treating time allocation as bet allocation: these methods work, but not because they are so good. They work because we are so naturally bad at reasoning about uncertainty.
Originally published , last updated .





