How Do You Evaluate Your Own Predictions?

In my last post, I wrote about Tetlock and Gardner’s 2015 book, Superforecasting, which covered the findings of Tetlock’s, Barbara Meller’s and Don Moore’s Good Judgment Project — a forecasting tournament and research program that ran from 2011 to 2015.

The core idea of last week’s post was to place Superforecasting against the consensus view that uncertainty cannot be modelled. Tetlock and co’s research gives us a good empirical basis on which to think that forecasting is possible. But how, exactly, do they do it?

This post provides a comprehensive summary of the technique that Tetlock and Gardner presents in Superforecasting. It is divided into two parts: part one (this week) is about the rules and evaluation criterion that GJP uses to evaluate forecasters. I've presented this in the context of an interested practitioner; I'm assuming you might want to improve forecasting decisions in your own life, but you don't have the time to implement a rigorous forecasting tournament in your organisation.

Part two, due next week, is about the actual techniques that Superforecasters use to achieve their results.

The rules of forecasting

GJP demands that forecasters make predictions according to a few rules, each of which are designed to prevent a number of problems that crop up whenever humans make predictions about the future.

We’ll take a quick look at those problems in a bit, but the rules first:

1. A forecast must take the form of an unambiguous yes or no statement. For instance, “Tesla is doomed” is a bad forecast, because it leaves room for ambiguity: what does ‘doomed’ mean? Does it mean that Tesla would go bankrupt, sunk by its oppressive debt burden? Or does it mean that Tesla would ultimately lose against its automotive rivals in the race for long-term electric car dominance? One might imagine a forecaster predicting doom, and then changing her mind on the underlying reason after the fact. Therefore, a forecast must be specific if the forecaster is to be fairly evaluated. For instance, “Tesla will fail to make its next debt repayment” is a better forecast than “Tesla is doomed” — it pins the forecaster down to an unambiguous issue.
2. A forecast must have a specific deadline. If I say “Tesla will go bankrupt”, and a year passes, I am able to say “Well, it hasn’t gone bankrupt yet, but it will eventually!” This is yet another way for forecasters to weasel their way out of a bad prediction. The solution: all forecasts must have a specific deadline attached, after which the prediction may be unambiguously evaluated: “Tesla will go bankrupt by 31 December 2020”.
3. A forecast should contain a probability estimation. The future is fundamentally uncertain, and forecasters should be allowed to express their uncertainty. So a forecaster is allowed to say “I think there’s a 60% chance that Tesla will go bankrupt by 31 December 2020.” If they don’t believe Tesla would go bankrupt, they should be allowed to pick 40%. (In this system, 50% is ’50-50’ — that is, you don’t know and think it could go either way). This rating becomes important for scoring in a bit, as we will soon see.
4. That probability estimation may be revised frequently. Tesla is expected to release their next earnings report on the 29th of January, 2020. A forecaster is allowed to change her estimation after this event — and, really, after any new development that might affect her appraisal of Tesla’s financial health. If Tesla’s earnings report uncovers a nasty surprise, for instance, the forecaster may revise her 0.6 estimation upwards to 0.63, or 0.69, depending on the severity of the surprise. All subsequent updates are taken into account when evaluating the forecaster’s score.

Why these rules? Tetlock and Gardner spend the first half of Superforecasting detailing how GJP’s researchers settled on these constraints. As it turns out, human brains are quirky; those quirks require guardrails to protect against:

• Humans are very good at lying to themselves. We have this particularly pernicious tendency to generate tidy explanatory narratives after the fact, thus forgetting the cloud of uncertainty when we were making our predictions. In Superforecasting, Tetlock tells us about the fall of the Soviet Union — and how both liberal and conservative experts constructed perfect little stories about the fall after the Union collapsed, as if it was the most inevitable thing in the world. (Tetlock: “My inner cynic started to suspect that no matter what had happened the experts would have been just as adept at downplaying their predictive failures and sketching an arc of history that made it appear they saw it coming all along.”)
• Ambiguous words mean different things to different people: “Osama may be hiding in that compound” might mean a 60% likelihood to you, whereas it might mean 75% to me. And these small differences in analysis matters: one imagines a commander who chooses to execute a mission if the collective judgement is above a 70% likelihood, but recalls the troops if his advisors assess the probability of success below 69%. Either decision leads us to two very different worlds.
• The lack of a deadline give forecasters wiggle room for deniability when the forecasted event fails to happen. Tetlock mentions a famous open letter sent to Ben Bernanke in November 2010, signed by a long list of economists and commentators. The letter argued that the Fed should stop quantitative easing because ‘it risks currency debasement and inflation.’ None of this ever happened in the years that followed, but it doesn’t matter — Tetlock points out that there was no deadline attached to the claims in the letter, so the signatories could always say “well, it hasn’t happened yet, but just you wait!”

The takeaway here is that if you want to be rigorous in improving your own predictions, step one is to adopt a set of rules that makes it really difficult for you to lie to yourself. Tetlock and co’s rules are as good a place to start as any.

Evaluating a forecaster

Let’s say that you adopt the GJP’s forecasting rules, and you begin recording your predictions for work. A fundamental question remains: how do you evaluate your skill as a forecaster? Without an objective method to score yourself, improvement becomes difficult.

This scoring problem is a lot trickier than you might think. Consider a weatherman who says that there’s a 70% chance of rain tomorrow. If it does rain tomorrow, we nod and smile and conclude that the weatherman was a good forecaster. But if it failed to rain, we might conclude the weatherman was wrong, and that no judgment of his should be trusted going forward.

Of course, we know this isn’t how probability judgments work. We could just happen to be living in the 30% of universes where it didn't rain. Our evaluation of the weatherman thus becomes more difficult: it seems like the only way to evaluate the weatherman on a single forecast is to replay the day hundreds of times, and see if 70% of those replays result in a rainy day.

We can’t do that, of course — we don’t have superpowers. But the literature on weather forecasting points us to something that serves as a good approximation: if we record the weatherman’s predictions on hundreds of days for a long-enough period of time, we may see if it really does rain 70% of the time, every time he says that there’s a 70% chance of rain.

This intuition is the basis on which Tetlock, Mellers and Moore built their evaluation criteria in the Good Judgment Project. A forecaster is evaluated on their overall performance across many predictions. Notice the implicit assumption here: even the best forecasters get things wrong — in fact, uncertainty pretty much guarantees that they will get some fraction of their predictions totally wrong. When Nate Silver forecasted a 71.4% win for Hilary Clinton in the 2016 US Presidential election, that didn’t mean that Silver was a dumbass when Trump won. It meant that uncertainty is a real thing, and that path-dependent, unpredictable events may cause previously-unimaginable events to occur. It meant that Silver got it wrong, but not to the degree that we should disregard his future forecasts.

What we want to get at is a scoring system that goes from ‘Oh, Silver is stupid’ to ‘Oh, Silver got this one wrong, he takes a sizeable hit to his overall forecasting score and goes from an A+ performer to an A.’ Ideally we want a scoring system that rewards or punishes the forecaster at the level of their confidence: if the forecaster is confident and predicts something at 90% probability, we want them to be rewarded handsomely if the event comes to pass, and to be punished harshly if they get it wrong; conversely, forecasters who are timid and predict events at 0.4 or 0.6 should’t be rewarded nor punished very much.

In simpler terms, we want to reward forecasters who a) make forecasts that coincide with the objective base rates of events and b) are highly confident when they do get things right. The first feature is called calibration, and the second feature, resolution.

The way the GJP calculates this is to use something called a Brier score, which is given by this formula:

$$BrS = \frac{1}{N}\sum\limits _{t=1}^{N}(p_t-x_t)^2 \,\!$$

where \(x_t\) equals \(1\) if the outcome occurs, and \(0\) if the outcome does not occur. \(p_t\) is the probability judgment from the forecaster. The Brier score is a number between \(0\) and \(2\); the lower the number, the better.

Here’s an example to make the scoring system clearer. Let’s say that my rating is 0.9 for “Tesla will be bankrupt by 31 December 2020” — that is, I predict to the tune of 90% that Tesla will be bankrupt when 31 December 2020 comes around. On the 1st of January 2021, we check to see if Tesla is bankrupt. If Tesla is bankrupt, \(x = 1\). My 90% prediction is great, and I’m rewarded handsomely: \((0.9-1)^2 = 0.01\), a fantastically low Brier score. But if Tesla isn’t bankrupt, \(x = 0\), and my Brier score is \(0.81\), a much higher (and more terrible) rating. My Brier score for this one prediction is much lousier if I had predicted at, say, 60% — which is as it should be. You are rewarded more when you are confident (and right), and rewarded less when you are timid in your predictions.

I am also allowed to update my prediction over time. Whenever news about Tesla comes out, for instance, I should be able to revise my 90% prediction upwards or downwards. Each time I do so, I record my revised forecast as an additional forecast (leaving the original forecast and previous updates as is). Then, on 1st January 2021, the collection of all my forecasts are aggregated into a Brier score for that particular question. In the GJP, the number of updates for a typical superforecaster was more than 16 per question — meaning thousands of forecasts made for hundreds of questions over the course of a given year.

Nuances of the Brier score

There are a couple of interesting nuances to this scoring method that deserve a closer look.

The first is that the Brier score is really more useful in its decomposed form (Murphy & Wrinkler, 1987). That is, you should evaluate your calibration and resolution to see how you’re doing on both measures. As a reminder:

• Calibration: are your predictions equivalent to the objective base rates of events? This is like the weatherman saying that there is a 70% chance of rain, and actually observing a 70% probability of rain over time. In practice, you are considered well-calibrated if your average confidence is equal to your % correct. In the context of the GJP, you are considered over-confident if your average confidence > your % correct, and under-confident if your average confidence < your % correct.
• Resolution: when you did get those forecasts right, how confident were your predictions? Good resolution means that you were decisive: that when you got your predictions correct, you made them at a confidence of between 70% and 90% (or 10%-30%), resulting in large gains in your overall Brier score. Bad resolution means that when you got your predictions right, you stuck to a timid band of 40%-60%, meaning you never won big bumps to your overall score.

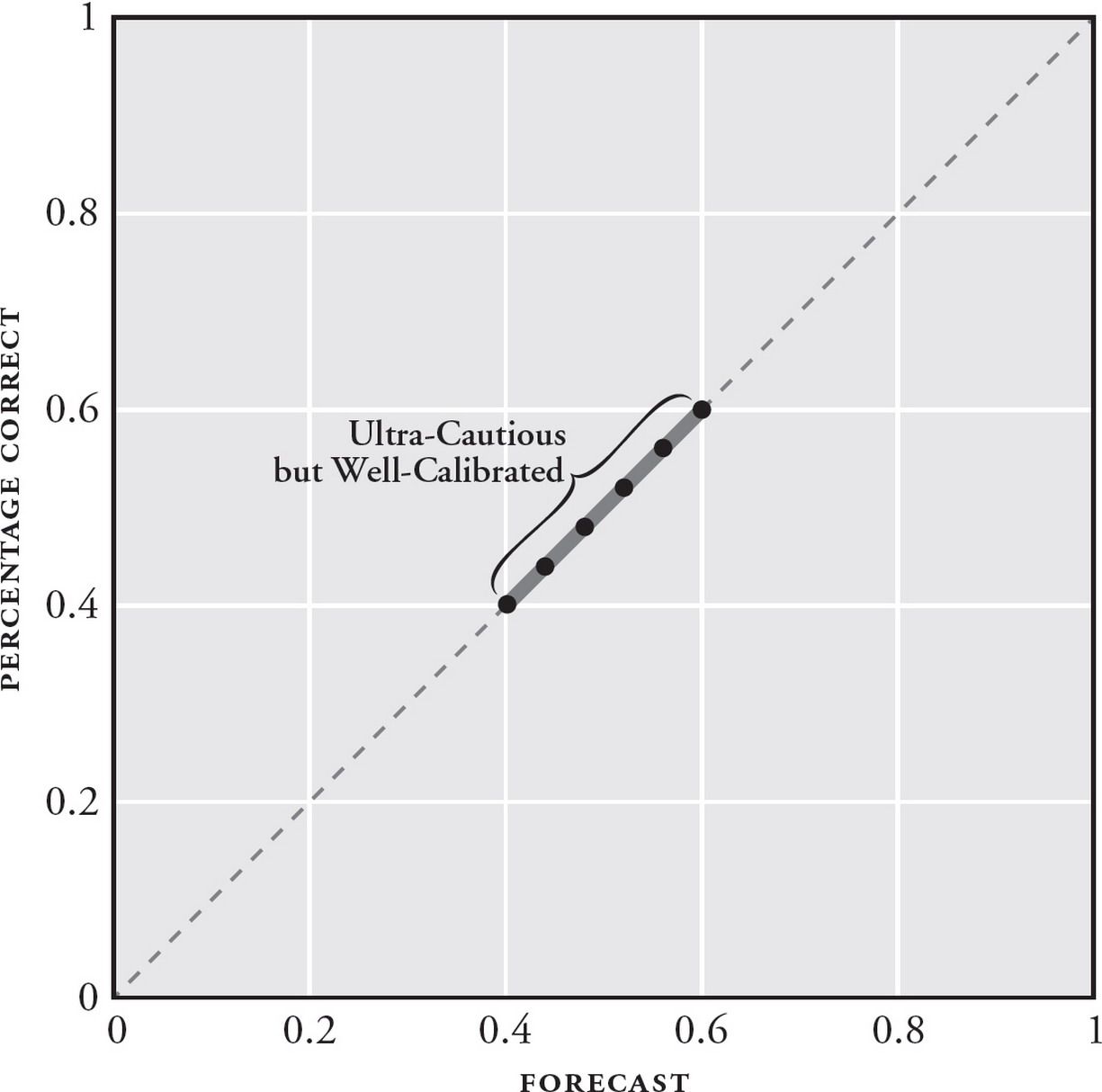
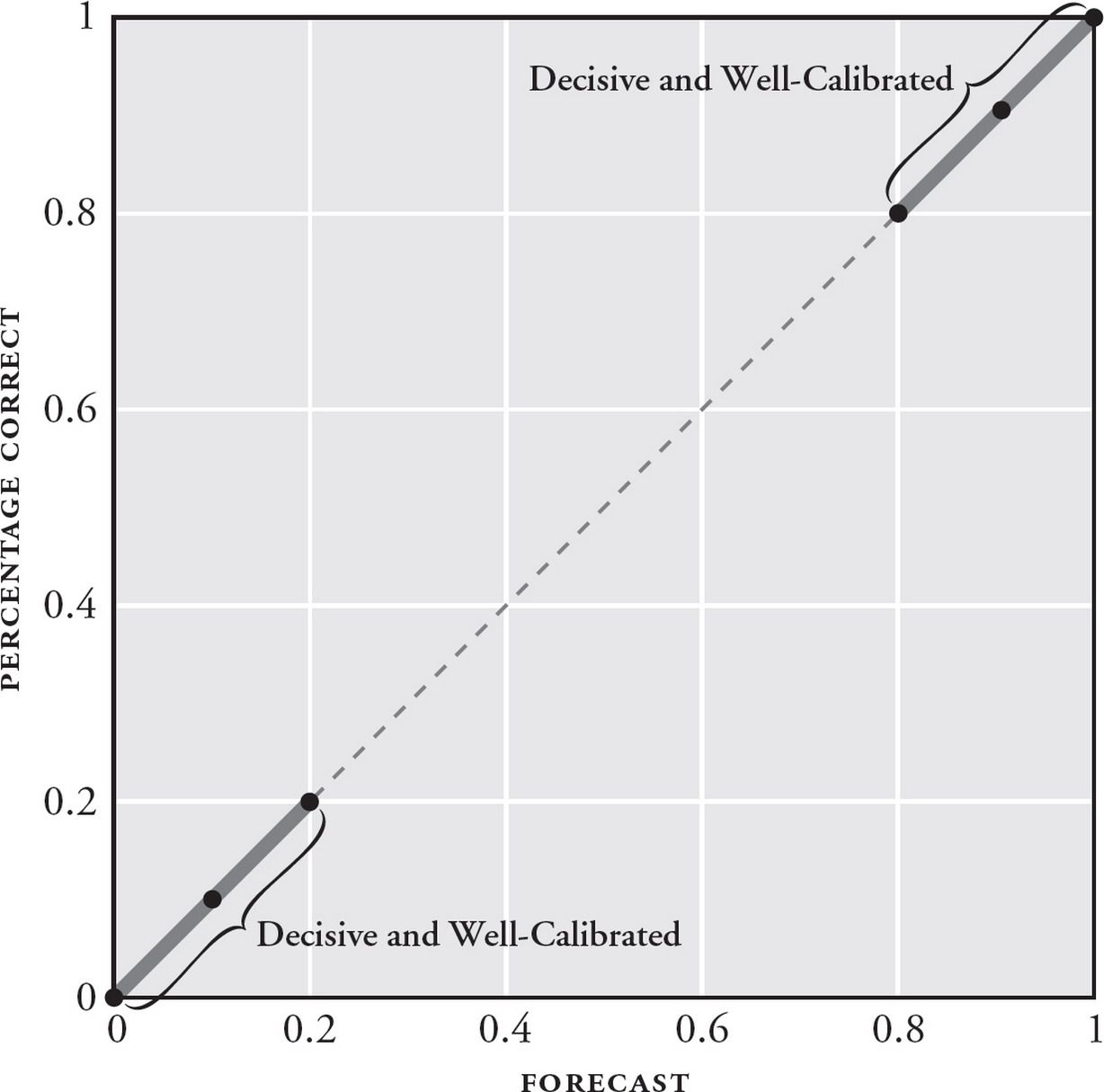
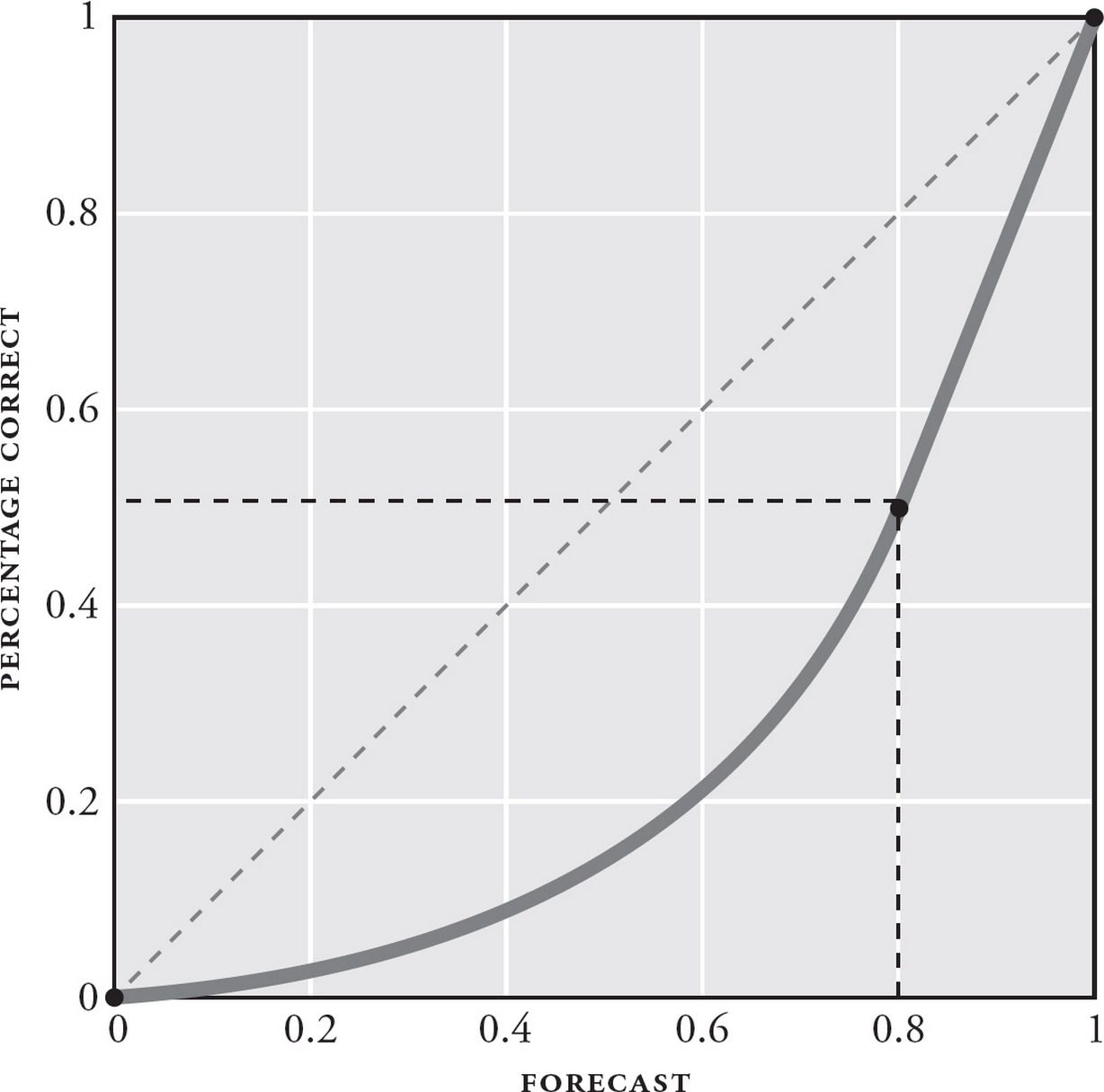
In the context of the GJP tournament, the best forecasters were those who were confident and right … which often meant taking a portfolio-approach to their predictions.

Tetlock notes that several forecasting questions are more difficult due to underlying uncertainty — anything more than one year out, for instance, resulted in wackier outcomes; forecasts for oil prices were another (incredibly notorious!) example — because oil prices are affected by too many factors in a complex adaptive system. Smart forecasters kept their bets timid for those, never straying outside the 40-60% range. Conversely, they made stronger, more confident predictions for forecasts that seemed more tractable.

The second nuance here is that overall Brier scores cannot be used to compare between different forecasters … if those forecasters made predictions on different things. This is easily demonstrated by extending our example of oil prices being difficult, above: if I had a group of forecasters make predictions on oil-price related questions, their overall scores will be lower than a group of forecasters who made predictions on more tractable political questions. The former (oil prices) are notoriously difficult to predict, while the latter (election results) have been shown to be more predictable given good poll data. This follows from our observation that different questions have different levels of uncertainty built-into them. If you want to compare between forecasters, you really do want everyone to be tested on the exact same set of questions.

The third nuance follows from the second, and is more important for practice: because forecasting performance depends on the ‘uncertainty level’ or difficulty of the specific forecasts, you can’t determine what a ‘good’ Brier score is for a given set of predictions without comparing within a cohort of forecasters*. Or, to put this another way: there is no one ‘good’ Brier score.

(* Tetlock covers one other way in his book, which is to compare against “mindlessly predicting no change”. But this isn’t universally applicable).

Perhaps we should make this clearer. Let’s say that you’ve started a GJP-style prediction scoring program for yourself. You’ve picked a domain you want to do better in — let’s say stock picking, which is well-suited to this scoring process. After a year, you make 200 predictions and score yourself … and come up with a Brier score of 0.23. Is this a good score or a bad score?

The answer is: well, you can’t know. Perhaps it is a terrible score, and it is possible to do much better than 0.23. Or perhaps the uncertainty associated with stock picking in your particular situation is very high, so you can’t do much better than 0.21 (in which case, 0.23 is an amazing score!). The only way to know is to recruit a large group of forecasters alongside you, ask them to make predictions on exactly the same things that you did at the exact same time, and then observe the top percentile scores in order to compare yourself to that.

This isn’t very practical, of course. What is more doable is to adopt the rules of GJP forecasting, and then apply it as a process to guard against self-delusion. Tetlock and Cerniglia argue that even if you only adopt GJP-style rules, this is a significant step up compared to the ‘vague-verbiage’ forecasting that analysts in finance are so used to doing.

Applying Superforecasting To A Real World Domain

I’ve spent a lot of time on this blog arguing that we shouldn’t fetishise ‘techniques from finance’ if we work in a ‘regular’ domain. If, for instance, you seek to improve your geopolitical forecasting or your stock analysis — sure, these domains are ‘irregular’; you may study Tetlock and Kahneman and Buffett and apply their techniques with ease. But if you want to improve in regular domains like management and programming and chess, you’re probably better off looking at ways to build taste, skill, and intuition — things that are rooted in good old pattern-recognition.

I am a programmer and a solopreneur; previously, I ran the engineering office in Vietnam for a Singaporean company. I’ve mostly worked in regular domains. This meant that I could judge most of my decisions by their outcomes, not by the process with which they were made. I could hone my intuitions through trial and error. I could focus on expertise at the expense of sophisticated analysis.

In 2016, when I first read Superforecasting, I assumed that there wouldn’t be many opportunities to test GJP-style forecasting — at least, not for the early stages of my career. But an interesting opportunity presented itself a few weeks ago, shortly after I read Tetlock and Cerniglia’s paper on using the Brier scoring method to evaluate the forecasting decisions that underpin stock-picking.

I had been helping a friend’s company with their marketing for a couple of months. At some point I decided that I was doing it all wrong; the first step in coming up with an effective marketing strategy is to deeply understand your customer. So I started listening to hours of sales calls over a series of weeks.

About 20 hours in, I began to develop an intuition for ‘good-fit’ customers — a gut feel for which customers were likely to close, and which were not. In other words … I began to make predictions.

I didn’t trust myself. I was relatively new to marketing, and terribly new to the field of business intelligence (which was the industry my friend’s company operated in). Tetlock and Cerniglia’s paper offered me an intriguing path forward — what if I started scoring my predictions? At the end of every sales call, I would write my probability estimation for the deal, along with my reasoning for that estimation. The sales cycle for this company was relatively short — a couple of months, tops. I could aggregate most scores within a quarter.

I began scoring my intuition slightly over two months ago. As expected, my scores have been incredibly bad. But the process itself has almost immediately proven useful — by introducing even a bit of rigour around my research, I started observing things that weren’t obvious to other members within the company. Shortly afterwards, I wrote a document that profiled some of the patterns I was seeing and spread it throughout the org. (I said I was only 70% confident in my observations, and detailed a number of potentially disconfirming cases).  The document currently functions as a working hypothesis for their go-to-market efforts; several salespeople think there’s merit — and so we’re currently validating large bits of it.

Is the Brier process a powerful method for scoring predictions in this field? I’m not entirely sure. It could be that the bulk of the benefit was in the rigour of the process, not the process itself. I’ve talked to more experienced marketers; to a person, they have all relied on their intuition in building an ideal persona and an ideal buyer’s journey in their heads. Marketing appears to be a regular domain.

Tetlock and Cerniglia argue that it’s the acceleration in learning and evaluation that helps — and they go one step further and argue that this should result in superior investing outcomes, because skilled forecasters revert to the mean more slowly than unskilled ones. What I will say, however, is that I’m less able to kid myself about my gut feelings ever since I started scoring my predictions. This in itself makes the process worth it to me — it doesn’t take much time, after all, to record a probability estimation alongside my rough-sketch analysis after each call.

It’ll probably take a few more quarters before I can report substantively on the exercise. But for now, I like what I’m seeing. If you do analysis of any kind, and you find yourself making predictions about near future events — that is, tractable predictions, not crazy things like the price of wheat in 2051 — then I think you might want to consider some of the ideas presented in this piece.

Next week, we’ll look at the techniques that superforecasters have used in the GJP — and follow up on an interesting question: just how important is overcoming cognitive bias in forecasting, anyway?

Note: this post is part of The Forecasting Series. The next post is available here: How The Superforecasters Do It.

Originally published 17 December 2019, last updated 12 January 2020.