This is a story that long-time readers of Commonplace would know.
In 2010, IARPA (Intelligence Advanced Research Projects Activity — basically, ARPA, but for the intelligence community) — started a research initiative called the Aggregate Contingent Estimation Program. ACE was a competition to determine the best ways to ‘elicit, weight, and combine the judgment of many intelligence analysts’, and it was motivated by IARPA’s desire to know how much money, exactly, they were wasting on geopolitical analysis. In the beginning, it consisted of five competing research programs. Within two years, only one survived: this was Phillip Tetlock, Barbara Mellers and Don Moore’s Good Judgment Project.
The GJP was a forecasting tournament. It asked individual participants questions like “What are the odds that Greece would leave the Eurozone by the end of 2011?” and “What are the odds that Tesla declares bankruptcy by the end of 2021?” — questions asked months in advance of the event dates. To these prompts, you would respond with a probability estimation — 0.9 meant you were pretty damned sure Greece would leave, while 0.5 meant you were on the fence; 0.1 meant you were sure Greece would stay put. Individual forecasters were evaluated according to something called a Brier score: this rewarded you handsomely the more confident you were (you got a huge bump if you said 0.9 and Greece did leave the Eurozone) but also a huge punishment if you were confident and the result you were betting on didn’t happen (e.g. you said 0.9 and Greece didn’t leave). The researchers quickly discovered that a small group of participants were very good at predicting the future — they called these people ‘superforecasters’ — and then spent quite a bit of time studying what these individuals did differently from the rest.
Over time, the program runners began to realise that the GJP was a fantastic test bed for all sorts of interesting judgment and decision making questions. For instance, one question you could reasonably ask is: “Are there ways to improve forecasting performance for the average forecaster?”, followed by Daniel Kahneman’s: “Do superforecasters have less cognitive biases than normal forecasters? And if they do (and it turned out they did show less cognitive bias!) — are these people different because they did things differently, or are they different because they are different types of people?” (answer: yes, a bit of both) and the logical next question: ‘Are there ways to reduce cognitive biases amongst forecasters?’
To that question, the researchers discovered three interventions that worked:
- Training — At the beginning of the tournament, the researchers provided forecasters with a short presentation about best practices: they taught people how to think about probabilities, where to get probabilistic information, how to average professional forecasts, and then they presented participants with a list of common biases in human judgment. The goal: to reduce cognitive biases.
- Teaming — Put forecasters in teams, with an online forum to discuss each prediction. The goal: to prevent biases such as group think and failures to pool information.
- Tracking — Put forecasters together in teams with other forecasters of similar performance. The goal: to see if elite teams would be more accurate than regular teams.
In the end, the researchers were pleased with the results of all three interventions. They wrote up a number of research papers, talking up their achievements in improving forecasting performance; Phillip Tetlock wrote a popular science book called Superforecasting with Dan Gardner, which made a huge splash in a bunch of different domains. More recently, Tetlock and Joseph Cergniglia published a paper in the Journal of Portfolio Management about something they called the ‘Alpha-Brier Process’ — a method to accelerate learning in active investment management. And the GJP authors and their collaborators crowed about the power of training interventions to reduce cognitive bias (Chang et al, 2016), and marvelled at the abilities of superforecasters at picking up subtle signals (Mellers et al, 2015).
Except that it turned out most of these interventions didn’t work by decreasing cognitive biases or increasing detection of subtle signals; they worked by tamping down on noise.
The Paper
The reason I said long-time Commonplace readers would be familiar with this story is because I wrote a series about Superforecasting and the Good Judgment Project at the end of 2019. If you want to save yourself some time chasing down books and papers, go and read that series — I’ve made it as comprehensive as I possibly could.
At the end of my Superforecasting summary, I wrote:
In the years since the GJP concluded, Barbara Mellers has continued to dig into the data generated by the forecasting tournaments — this time with an eye to explain why the interventions worked as well as they have.
The original intention of all three interventions was to reduce cognitive biases, in line with the Kahneman and Tversky research project of the time. But this didn’t turn out to be the case. In a recent interview, Mellers and INSEAD professor Ville Satopӓӓ explained that they went back and applied a statistical model to the entire 2011-2015 GJP dataset, designed to tease out the effects of bias, information and noise (BIN) respectively. Satopӓӓ writes:
How does the BIN model work? Simply put, it analyses the entire “signal universe” around a given question. Signals are pieces of information that the forecasters may take into account when trying to guess whether something will happen. In formulating predictions, one can rely upon either meaningful signals (i.e. information extraction) or irrelevant signals (i.e. noise). One can also organise information along erroneous lines (i.e. bias). Comparing GJP groups that experienced one or more of the three interventions to those that did not, the BIN model was able to disaggregate the respective contributions of noise, information and bias to overall improvements in prediction accuracy.
This explanation isn’t satisfying to me, but apart from an interview with Mellers and Satopӓӓ, there’s not much else to go on — the paper is still in progress, and hasn’t been published.
But the conclusions are intriguing. Here’s Satopӓӓ again:
Our experiments with the BIN model have also produced results that were more unexpected. Recall that teaming, tracking and training were deployed for the express purpose of reducing bias. Yet it seems that only teaming actually did so. Two of the three — teaming and tracking — increased information. Surprisingly, all three interventions reduced noise. In light of our current study, it appears the GJP’s forecasting improvements were overwhelmingly the result of noise reduction (emphasis added). As a rule of thumb, about 50 percent of the accuracy improvements can be attributed to noise reduction, 25 percent to tamping down bias, and 25 percent to increased information.
The authors have little to offer by way of actionable insight. In their interview, they suggest that using algorithms would improve noise reduction, but they also note that machines aren’t great at the multi-perspective synthesis that human superforecasters are so great at. It’s unclear to me if this is actionable. I’ll wait for the paper and report back to you once that’s out.
That paper is titled Bias, Information, Noise: The BIN Model of Forecasting. It was completed on the 19th of February, 2020, and was published to SSRN in April last year — all of which I completely missed out on, because it happened right smack in the middle of the global lockdown.
The paper has two primary contributions. The first is the BIN model itself, which is a statistical model designed to tease out the respective contributions of bias, partial information, and noise to forecasting performance — at least within the context of the GJP. The second is what the authors use the BIN model to do: that is, to measure the degree their interventions improved each of the three elements. How much did tracking and teaming tamp down on cognitive bias? And how much did it help forecasters reduce noise?
The answer is exactly what Satopӓӓ reported in his original INSEAD piece:
- All three interventions reduced noise. Only one intervention — teaming — reduced cognitive biases. This was despite the fact that the GJP researchers targeted cognitive biases with their interventions — which is a little bit like aiming for one target in an archery range and hitting a bullseye on the lane next to it. The researchers said they were taken aback by this result, and that it demanded a re-evaluation of the findings from their prior work.
- Across all interventions, the rough breakdown of accuracy improvements are as follows: 50% to noise reduction, 25% to tamping down on bias, and 25% to increased information.
We’ll talk about what this means in a bit; for now, I want to give you a sketch of the BIN model in action.
How The BIN Model Works
The formal definition of noise is ‘unpredictable, nonsystematic error’.
Imagine that in order to make a forecast, you observe a set of signals over time. Some signals are useful, and they cause you to update your forecast. This is partial information. Other signals are irrelevant, and may cause you to update erroneously. This is noise. And some signals you misinterpret due to cognitive bias — which should lead to judgment drift in a particular direction. This is bias. The differences between noise and bias is best illustrated using the following diagram:
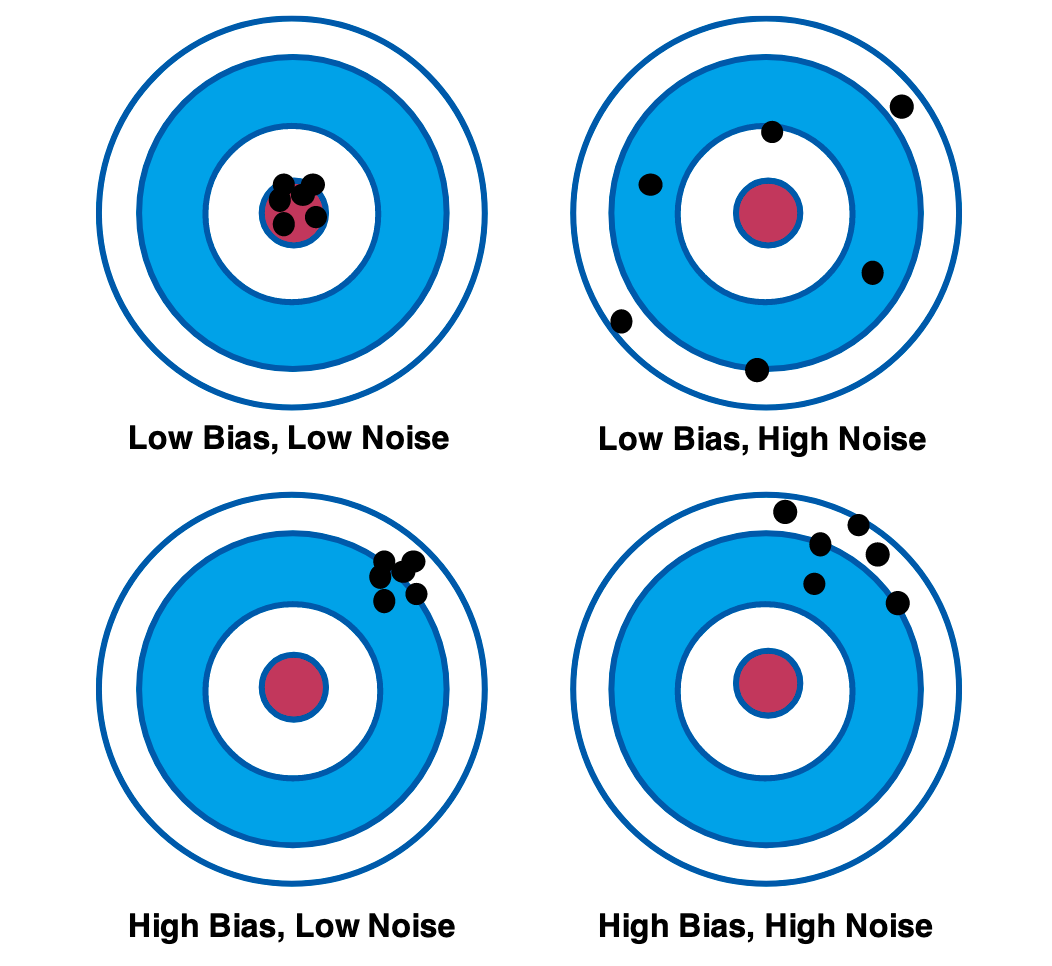
Keep this diagram in mind; it’ll come in handy in a bit.
In 2016, Daniel Kahneman co-authored a famous article in the Harvard Business Review titled Noise: How to Overcome the High, Hidden Cost of Inconsistent Decision Making. The article is useful because it gives us several additional examples of noise in decision-making. Kahneman et al begin their argument with a quick comparison between bias and noise, using a bathroom scale as an example:
When people consider errors in judgment and decision making, they most likely think of social biases like the stereotyping of minorities or of cognitive biases such as overconfidence and unfounded optimism. The useless variability that we call noise is a different type of error. To appreciate the distinction, think of your bathroom scale. We would say that the scale is biased if its readings are generally either too high or too low. If your weight appears to depend on where you happen to place your feet, the scale is noisy. A scale that consistently underestimates true weight by exactly four pounds is seriously biased but free of noise. A scale that gives two different readings when you step on it twice is noisy. Many errors of measurement arise from a combination of bias and noise. Most inexpensive bathroom scales are somewhat biased and quite noisy.
But of course a bathroom scale is a trivial example. A more interesting example is to take, say, a loan officer at a bank, receiving an application in their inbox. In theory, the same application submitted to the same officer on Monday and on Wednesday should result in the same decision (“Hi! Mr Yang, I’m pleased to say that we’ve approved your loan of $50k at 3.7% per annum …”). Similarly, the same application submitted to different officers of the same bank should in theory result in the same decision: an approval, or a rejection, and on the same terms.
In practice, when you go looking, there turns out to be fair amount of variability in the outcome. Perhaps the loan officer broke up with his girlfriend on Wednesday, and zipped through his inbox in anguish. Perhaps the officers in bank branch A are more paranoid than the officers in bank branch B. Kahneman and his co-authors argued that variability can be measured relatively easily in any decision making organisation; more importantly, this variability may result in millions of dollars of invisible costs in higher risk domains like loan underwriting or investment sizing. Such random variability in decision making outcomes is also called ‘noise’.
These examples give you a better idea of what it means to ‘tamp down on noise’ in the context of the Good Judgment Project. You can sort of imagine that a superforecaster is simply someone who doesn’t over-react to the latest Twitter outrage; similarly, they know enough to stay away from their forecasting dashboards right after a breakup. More intriguingly, the researchers show that all three of their interventions encourage such ‘disciplined’ behaviour.
How the BIN model is able to decompose forecasting performance into the three elements is more complicated to explain. I’ve spent a few days working my way through the math, and I still don’t understand big chunks of it. (I asked a few friends to help me with this, of course, and felt bad about my lack of statistical sophistication until one of them explained that the technique used by the paper was taught in university, but only in a fourth year undergrad stats class — and I never progressed beyond the required first year classes in the stats department. For those of you who are math-savvy, the BIN model falls into the category of techniques known as probabilistic graphical models; the consensus amongst my more proficient friends is that the model is ‘simple’ and ‘eh, slightly contrived’.)
So here’s my best stab at an explanation.
Imagine that a real world event either happens or doesn’t happen. We call that real world event $Y$, where $Y = 1$ if the event happens and $Y = 0$ if the event doesn’t. The outcome of $Y$ is determined by a normally distributed random variable $Z^{*}$ such that $Y = 1(Z^{*} > 0)$, where the indicator function $1(E)$ is true if $E$ is true. This is simply a fancy way of saying that the odds of $Z^{*} > 0$ is the real world probability that the event would happen — if, for instance, there is a $0.8$ chance that Biden wins the 2020 US elections, then $\mathbb{P}(Z^{*} > 0) = 0.8$, and going back in time and replaying reality a million times should mean that in 80% of the universes, Biden should win; a small 20% of universes would see him lose.
Of course, we can’t directly calculate $Z^{*}$, or even $\mathbb{P}(Z^{*} > 0)$. What we do have is $Y$ — which is either 1 or 0, depending on the results of the real world event — and $p_0$, which is the probability estimation the forecaster makes for that event. Let’s say that $p_0$ is based on the normally distributed variable $Z_0$, which represents the forecaster’s interpretation of the signals.
With these definitions in place, the authors argue that we may calculate the following:
- Bias, $\mu_0$, is $\mathbb{E}(Z_0) - \mathbb{E}(Z^*)$, or the difference between the means of $Z_0$ and $Z^{*}$
- Information, $\gamma_0$, is $Cov(Z_0, Z^{*})$, or the covariance between $Z^{*}$ and $Z_0$
- Noise, $\delta_0$, is $Var(Z_0) - Cov(Z_0, Z^{*})$, which is the remaining variability of $Z_0$ after removing all covariance with $Z^{*}$.
Or, to put it succintly, $Z^{*}$ and $Z_0$ follow a multivariate normal distribution:
\(\begin{pmatrix}Z^* \\\ Z_0 \end{pmatrix} \mathtt{\sim} \mathcal{N} \left(\begin{pmatrix} \mu^* \\\ \mu^{*} + \mu_0 \end{pmatrix}, \begin{pmatrix}1 & \gamma_0\\\ \gamma_0 & \gamma_0 + \delta_0 \end{pmatrix} \right)\)
How they actually go from probability forecast $p_0$ and event outcome $Y$ to the interpretation $Z_0$ (and therefore bias, information and noise) is beyond me; this is laid out in the equations on page 6 and 7 of the paper.
But the gist of the BIN model lie in the definitions above — bias is the difference between the means of $Z^{*}$ and $Z_0$; information is the covariance between $Z^{*}$ and $Z_0$ (the more $Z_0$ covaries with \(Z^{*}\), the more information the forecaster has about the event; perfect information effectively means that \(Z_0 = Z^{*})\), and noise is whatever is leftover after you subtract that covariance from the variance of \(Z_0\).
Armed with these definitions, the authors then examined each of the three interventions over the course of the GJP, comparing each intervention group against their respective control groups. The improvement breakdowns are as follows:
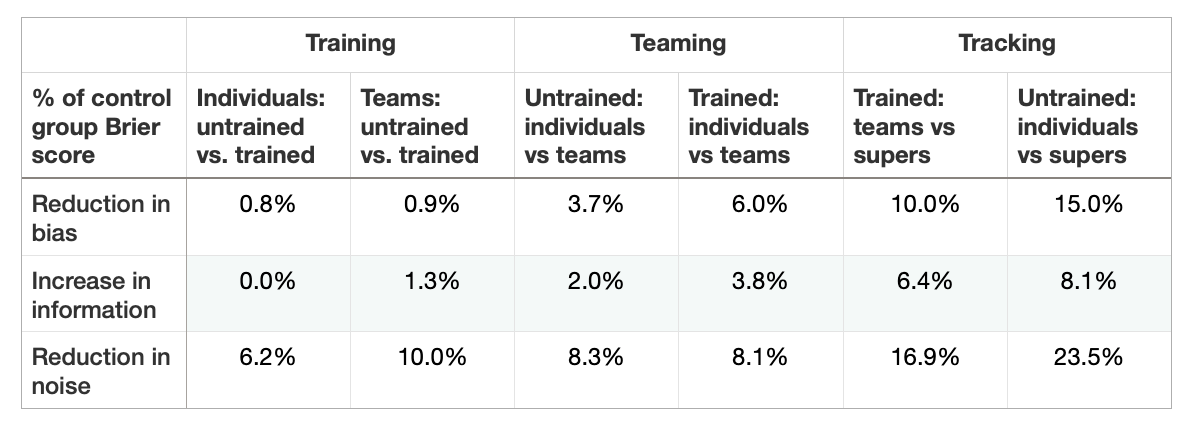
It’s worth asking: why is this the case? Why did most of the interventions tamp down on noise? The authors don’t really know. They have suspicions, of course: they suspect that teaming helped forecasters converge on more reliable crowd judgments, that debiasing training — which stresses the value of grounding initial probability judgments in base rates — stabilised forecasts. And they speculated that tracking superforecasters together should naturally lead to more reliable crowd aggregates, because of course they would — they were putting elites together, right? But then these explanations are post-hoc, liable to hindsight bias, and the researchers aren’t perfectly happy with any of them.
In the end, the authors conclude:
… the results (of this new paper) place qualifications on past portrayals of top performers (superforecasters) in both the scientific literature (Mellers et al. 2015) and in popular books (Tetlock and Gardner 2016). Earlier work had stressed the insightful ways in which top performers either extracted subtle predictive clues that others missed or avoided being gulled by pseudo-diagnostic cues that others were misled into using. Our data suggest that “superforecasters” owe their success more to superior skills at tamping down measurement error, than to unusually incisive readings of the news. Discipline may matter more than creativity here.
Takeaways
So what should we conclude from the BIN paper?
One obvious takeaway is that you’re probably going to get better decision making results if you target noise than you would if you targeted cognitive biases. One of the things that we’ve talked around, but not directly discussed, is this idea that fighting cognitive biases is just plain hard, and that you should be sceptical of most interventions designed to combat it. It turns out that there’s quite a bit of history behind this single statement, so let’s talk about that for a moment.
One of the most dispiriting positions that Daniel Kahneman — the father of the cognitive biases and heuristics research program — has had over the past few decades is that we can’t do much about our cognitive biases. At the end of Thinking: Fast and Slow, for instance, Kahneman writes:
What can be done about biases? How can we improve judgments and decisions, both our own and those of the institutions that we serve and that serve us? The short answer is that little can be achieved without a considerable investment of effort. As I know from experience, System 1 is not readily educable. Except for some effects that I attribute mostly to age, my intuitive thinking is just as prone to overconfidence, extreme predictions, and the planning fallacy as it was before I made a study of these issues. I have improved only in my ability to recognize situations in which errors are likely: “This number will be an anchor…,” “The decision could change if the problem is reframed…” And I have made much more progress in recognizing the errors of others than my own.
The way to block errors that originate in System 1 is simple in principle: recognize the signs that you are in a cognitive minefield, slow down, and ask for reinforcement from System 2. This is how you will proceed when you next encounter the Müller-Lyer illusion. When you see lines with fins pointing in different directions, you will recognize the situation as one in which you should not trust your impressions of length. Unfortunately, this sensible procedure is least likely to be applied when it is needed most. We would all like to have a warning bell that rings loudly whenever we are about to make a serious error, but no such bell is available, and cognitive illusions are generally more difficult to recognize than perceptual illusions. (emphasis added)
Kahneman’s full position is two-fold: first, you may attempt to overcome your cognitive biases, but that’s super hard and you shouldn’t expect much from the effort. Second, you have a higher chance of succeeding if you’re grappling with these biases at the level of an organisation (or team). This view lines up nearly perfectly with the literature: Arkes showed us in 1991 that cognitive biases aren’t as irresistible as perceptual illusions (unlike Kahneman’s assertion, above), and Lerner, Tetlock in 1999, along with the original GJP project, showed us that teaming can successfully reduce cognitive biases. The BIN paper arguably tells us the exact same thing — with the added caveat that only teaming reduced bias.
Of course, there has been a bit of a back-and-forth over this issue over the past four decades. Writer Ben Yagoda wrote an entertaining treatment of this argument over at The Atlantic in 2018; the summary of the disagreement is basically Kahneman going “I don’t think you can fight your cognitive biases in the real world”, and Richard Nisbett and his colleagues going “We disagree! We’ve done all sorts of training interventions that shows students improving on cognitive biases when tested!” and then Kahneman going: “Bah, tests! Tests are artificial! You go into a test knowing you’ll be tested; no such thing exists in the real world!”
The BIN paper arguably gives us more evidence that Kahneman was on the right path. Yes, debiasing training doesn’t really cause your biases to go away. Yes, only teaming works to arrest cognitive biases. But perhaps that’s ok — if teaming, tracking, and training help forecasters improve their performances by tamping down on noise, does it matter that it’s not cognitive biases that’s been targeted?
Kahneman has been busy in the past few years. After he wrote his 2016 article on noise, he began experimenting with ways to reduce it in all sorts of decision making environments. I’ll cover some of those techniques in my next blog post. The GJP researchers themselves state that they’re interested in uncovering the exact mechanisms with which their interventions reduced noise. The idea here is intuitive: if we understood the underlying mechanisms, the logic goes, we would be able to design new interventions, with the express purpose of reducing nonsystematic decision error. The results of the BIN paper thus represent a compelling argument for going after noise reduction.
More importantly, it tells us what to pay attention to. It tells us that we should look to noise, not biases. It tells us that we should start watching the research on prescriptive noise reduction, at least in the field of judgment and decision making.
I’ve covered the Naturalistic Decision Making research field on Commonplace before — a community that embraces cognitive biases and uses them to enhance intuitive decision making. That community is diametrically opposed to Kahneman and company. But I think we’re slowly coming to the conclusion that cognitive biases aren’t really reducible. They exist as a quirk of our information processing architecture. In other words, fighting cognitive biases is in many ways going against the grain of the human mind; Kahneman himself says — of overconfidence — “it is built so deeply into the structure of the mind that you couldn’t change it without changing many other things”.
Targeting noise, on the other hand, feels like much lower hanging fruit.
As it turns out, Kahneman has a new book that’s due for publication in May this year. The title? Noise: A Flaw in Human Judgment.
If the sales of Thinking: Fast and Slow are anything to go by, we should expect this book to also become a bestseller. And we should expect noise reduction research to be a bigger thing in the coming years.
Originally published , last updated .





